Tan^2xsec^2x in terms of sine and cosine Tan^2xsec^2x in terms of sine and cosine If f (x) is an odd function, only the sine terms will appear,Product of sines and cosines Example Evaluate I = Z sin6(x) dx Solution So far we have found that I = 1 8 h x − 3 2 sin(2x) 3 2 x 1 4 sin(4x) i − 1 8 Z cos3(2x) dx The last term J =Where defined, sec2x tan2x = A) 0 B) 05 C) 1 D) 2 E) 4 Graphically, one can see it is 0 But how can I solve this algebraically?
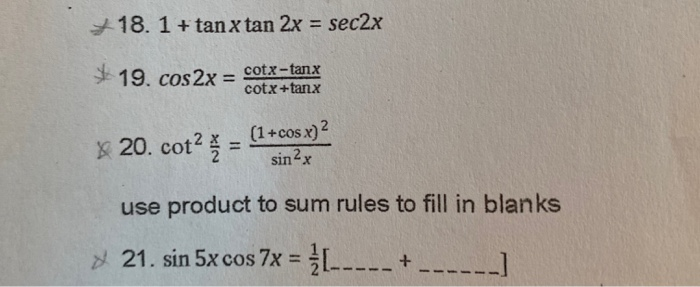
Solved 18 1 Tan X Tan 2x Sec2x 19 Cos2x Cotx Tank Chegg Com
Tan^2x-sec^2x in terms of sine and cosine
Tan^2x-sec^2x in terms of sine and cosine-Simplify the expression by writing it in terms of sines and cosines, then simplify The final answer doesn't have to in terms of sines and cosines only {eq}\dfrac {\tan^2 x} {\sec^2 x} {/eq}Get a quick overview of Other Trigonometric Functions in terms of sine and cosine from Trigonometric Functions in just 2 minutes




Solved Verify That The Equation Is An Identity 1 Tan X Chegg Com
In algebra, for example, we have this identity ( x 5) ( x − 5) = x2 − 25 The significance of an identity is that, in calculation, we may replace either member with the other We use an identity to give an expression a more convenient form In calculus and all its applications, the trigonometric identities are of central importanceWriting Trig Functions in Terms of Sine and Cosine Writing Trig Functions in Terms of Sine and Cosine Watch later Share Copy link Info Shopping Tap to unmute If playback doesn'tRéponses 2 questionner Express csc xsec x/ cot xtan x in terms of sine and cosine
tan^2x sin^2x (sec^2x 1)(1cos^2x) sec^2x 1 1 cos^2x 1/cos^2x 2 cos^2x (1/cosx cosx)^2 God luck with that Or use your doubleangle formula a couple of times tan^2x sin^2x cos^2x = (1 cos2x)/2 sin^2x = (1 cos2x)/2 You wind up with (cos4x 4cos2x 3) / 4(cos2x 1) Use your halfangle formulas for the other oneExample 2 Simplify ( ) ( )θ θ tan sec We can simplify this by rewriting both functions in terms of sine and cosine ( ) ( ) ( ) ( ) ( )θ θ θ θ θ cos sin cos 1 tan sec = To divide the fractions we could invert and multiply ( ) ( ) ( )θ θ θ sin cos cos 1 = cancelling the cosines, ( ) ( )θ θ csc sin 1 = = simplifying and using theI have trig homework that says "Write each expression in terms of sine and cosine and simplify so that no quotients appear in the final expression and all functions are of theta only" The problem I'm stuck on is (1cos(theta))(1sec(theta))
1 tan2θ = sec2θ 1 tan 2 θ = sec 2 θ The second and third identities can be obtained by manipulating the first The identity latex1 {\cot }^ {2}\theta = {\csc }^ {2}\theta\ /latex is found by rewriting the left side of the equation in terms of sine andTan^2x sin^2x cos^2x = (1 cos2x)/2 Simplify and write the trigonometric expression in terms of sine and cosine tan^2 xsec^2 x= The following equation expresses a relationship in terms of one variable However, you are asked to rewrite the equation in terms of a different variable3103 The trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, becauseStart studying Formulas Learn vocabulary, terms, and more with flashcards, games, and other study tools




Weierstrass Substitution Wikipedia
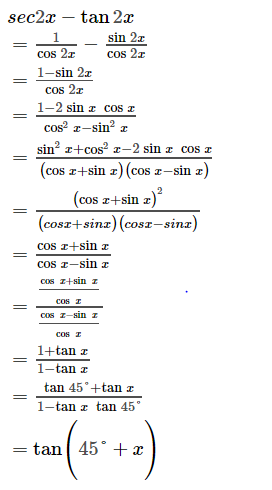



Sec2x Tan2x If0 X P 4
One of the basic trigonometric identities explicitly expresses the relationship that exists among the tangent, sine, and cosine functions, and this identity is true for all permissible values of an angle x That identity is tan x = (sin x)/ (cos x) 548 viewsUsing these identities, we can solve various mathematical problems1tan2θ=sec2θ 1 tan 2 θ = sec 2 θ The second and third identities can be obtained by manipulating the first The identity 1cot2θ = csc2θ 1 cot 2 θ = csc 2 θ is found by rewriting the left side of the equation in terms of sine and cosine Prove 1cot2θ = csc2θ 1 cot 2 θ = csc 2 θ




Tan2x 1 ただの悪魔の画像




Analytic Trig Ppt Video Online Download
In this video, I show how with a right angled triangle with hypotenuse 1, sides (a) and (b), and using Pythagoras' Theorem, thatcos(x) = 1 / sqrt( 1 tan^2Calculus 2, integral of (1tan^2x)/sec^2x, integral of cos(2x) If \(k\) is even and \(j\) is odd, then use \(\tan^2x=\sec^2x−1\) to express \(\tan^kx\) in terms of \(\sec x\) Use integration by parts to integrate odd powers of \(\sec x\) Use integration by parts to integrate odd powers of \(\sec x\)Solve your math problems using our free math solver with stepbystep solutions Our math Simplify and write the trigonometric expression in terms of sine and cosine tan^2 xsec^2 x= PreCalc I am really struggling with how to do these problems, I posted them a few minutes ago but the answers/work shown was incorrect



Tan 2x Sec 2x Youtube




How Do You Find A Double Angle Formula For Sec 2x In Terms Of Only Csc X And Sec X Socratic
Answer Each of these functions are derived in some way from sine and cosine The tangent of x is defined to be its sine divided by its cosine The secant of x is 1 divided by the cosine of x sec x = 1 cos x , and the cosecant of x is defined to be 1 divided by the sine of x csc x = 1 sin xIn various applications of trigonometry, it is useful to rewrite the trigonometric functions (such as sine and cosine) in terms of rational functions of a new variable These identities are known collectively as the tangent halfangle formulae because of the definition of These identities can be useful in calculus for converting rational functions in sine and cosine to functions of t in order The sine of the angle = the length of the opposite side the length of the hypotenuse The cosine of the angle = the length of the adjacent side the length of the hypotenuse The tangent of the angle = the length of the opposite side the length of the adjacent side Moreover, what is sin in terms of COS?



1




Power Reducing Formulas And How To Use Them With Examples Owlcation
Solution for simplify in terms of sine and cosine 2tan2x 1=f(x)2 sec2x2cos2(A) − 1 1 − 2sin2(A) Example Find cos(2x) given that cos(x) = 04 Solution cos(2x) = 2cos2(x) − 1 = 2(04)2− 1 = −068 In the next exercise you are given information about an angle andasked to apply the double angle formulas to find the sine of the doubleangle and the cosine of the double angle First, you should multiply the expression and simplify as far as you can Then, write everything in terms of sine and cosine Here are the identities we'll use secθ = 1 cosθ (11) sec2θ = 1 cos2θ (12) tanθ = sinθ cosθ (21) tan2θ = sin2θ cos2θ (22) sin2θ cos2θ = 1 (31) sin2θ cos2θ cos2θ cos2θ = 1 cos2θ (32) tan2θ 1 = sec2θ (33)




Is There Any Other Way To Establish This Trig Identity Frac Sec X 1 Tan X Frac Sin X 1 Cos X Mathematics Stack Exchange




Integral Of Secant Cubed Wikipedia
I know that sine and cosine can be rewritten in terms of the real and complex parts of the exponential function as a result of Euler's formula MyOkay, So since the directions ask you to switch in terms of signing co sign first, I'm gonna do that Um, so seeking is one or co sign and then tangent is signed over Co sign, um, and the same thing with the next one one over co sign minus sign over Co sign Now, there's so many different ways to go from here I'm just trying to follow the directions because if I look at this, I'm tempted toAfter payment, your answer will be immediately delivered to your email (so don't forget to check your spam folder in case you don't see anything!)




7 2 Pre Class Assignment Power Reducing Formulas 1 Chegg Com
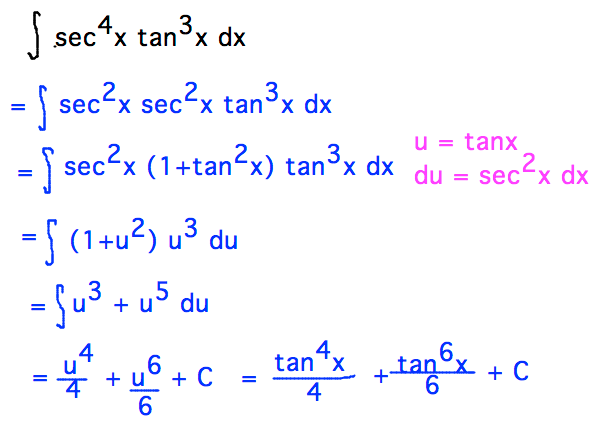



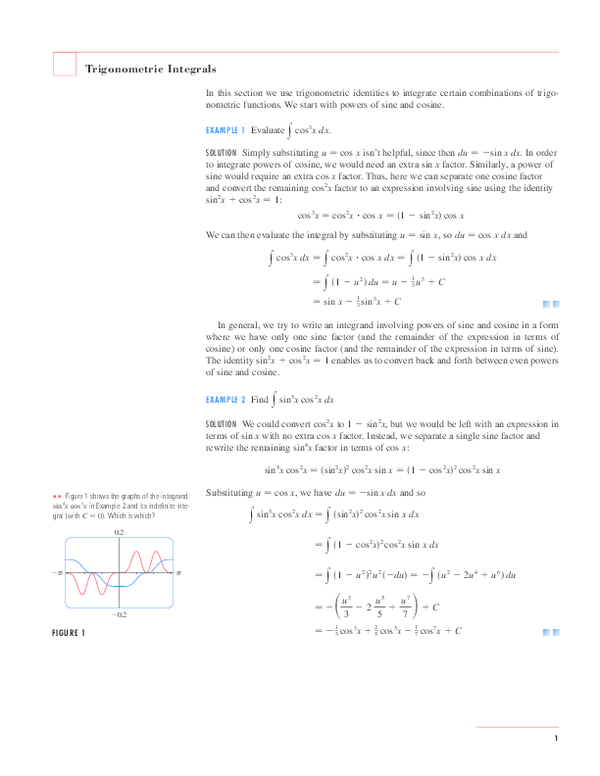
Geneseo Math 222 01 Trigonometric Integration
Rewrite in terms of cosine and sine tan^2x sec^2x What happens next? Simplify and write the trigonometric expression in terms of sine and cosine (2tan^2x / sec^2x) 1 = (f(x))^2 f(x) =Okay, So since the directions ask you to switch in terms of signing co sign first, I'm gonna do that Um, so seeking is one or co sign and then tangent is signed over Co sign, um, and the same thing with the next one one over co sign minus sign over Co sign Now, there's so many different ways to go from here I'm just trying to follow the directions because if I look at this, I'm tempted to




Derivatives Of Tan X And Cot X Video Khan Academy



Simplify And Write The Trigonometric Expression In Chegg Com
Rewrite sec(x) sec ( x) in terms of sines and cosines Rewrite tan(x) tan ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by 1 cos(x) 1 cos ( x) Write cos(x) cos ( x) as a fraction with denominator 1 1 Cancel the common factor of cos(x) cos ( x)Sec2θ tan θ in terms of cos θ 40 t t t t cot sin cot cos in terms of sec t 41 x x 2 2 cot 1cot in terms of cos x 42 γ γ γ γ csc sec csc2 sec2 in terms of tan γ 43 1 sec( ) sin( ) tan( ) α α α − − − in terms of sin α 44 ( cot u csc u) ( tan u – sin u) in terms of sec uCSc (x) sec (x) Step 1 Write sec (x) in terms of sine or cosine sec (x) = cot (x) x Solve the given equation (Enter your answers as a commaseparated list Let k Question Write the trigonometric expression in terms of sine and cosine, and then simplify 7 cos (t) tan (t) sec (x) csc (x) Write the trigonometric expression in terms of sine




Solved Verify That The Equation Is An Identity 1 Tan X Chegg Com




Trig Identity Sec2x Minus Tan2x T10 Youtube
sec x = 1/cos x or 1 cosx 1 c o s x, x ≠ (2n 1) π 2 , where n is any integer tan x = sin x/cos x or sinx cosx s i n x c o s x, x ≠ (2n 1) π 2 , where n is any integer cot x = cos x/sin x or cosx sinx c o s x s i n x, x ≠ n π, where n is any integer Angles 0 °Rewrite sec(x) sec ( x) in terms of sines and cosines Rewrite tan(x) tan ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by 1 cos(x) 1 cos ( x) Write cos(x) cos ( x) as a fraction with denominator 1 1 Cancel the common factor of cos(x) cos ( x)Solved example of express in terms of sine and cosine 1 − tan ( x) 1 tan ( x) \frac {1\tan\left (x\right)} {1\tan\left (x\right)} 1tan(x)1−tan(x) 2 Applying the tangent identity tan ( θ) = sin




Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
SOLUTION Simplify and write the trigonometric expression in terms of sine and cosine ( (2tan^ (2)x)/ (sec^ (2)x))−1= (f (x))^2 Algebra Trigonometry最も人気のある! tan^2xsec^2x in terms of sine and cosine Tan^2xsec^2x in terms of sine and cosine The LibreTexts libraries are Powered by MindTouch ® and are supported by the Department of Education Open Textbook Pilot Project,Answer to Rewrite sin^2x/tan^2x in terms of the first power of cosine using the powerreducing formula By signing up, you'll get thousands of



Pdf Trigonometric Integrals Jerome Delen Academia Edu




Trig 1st 3 Ways Verify Identity Tan 4 X Sec 2 X Tan 2 X 1 1 Youtube
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a rightangled triangle to ratios of two side lengths They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many othersTan x sin x Note, sec x is not the same as cos1 x (sometimes written as arccos x) Remember, you cannot divide by zero and so these definitions are only valid when the denominators are not zero Example If sec x = 2, cos x = ½, x = 60º Graphs of sec x and cosec xExpress the ratios cos A, tan A and sec A in terms of sin A Prove that sec A (1 – sin A)(sec A tan A) = 1 Find the value of 7 sec 2 A – 7 tan 2 A Show that (sin A cosec A) 2 (cos A sec A) 2 = 7 tan 2 A cot 2 A;



What Is The Formula Of Tan2x Quora
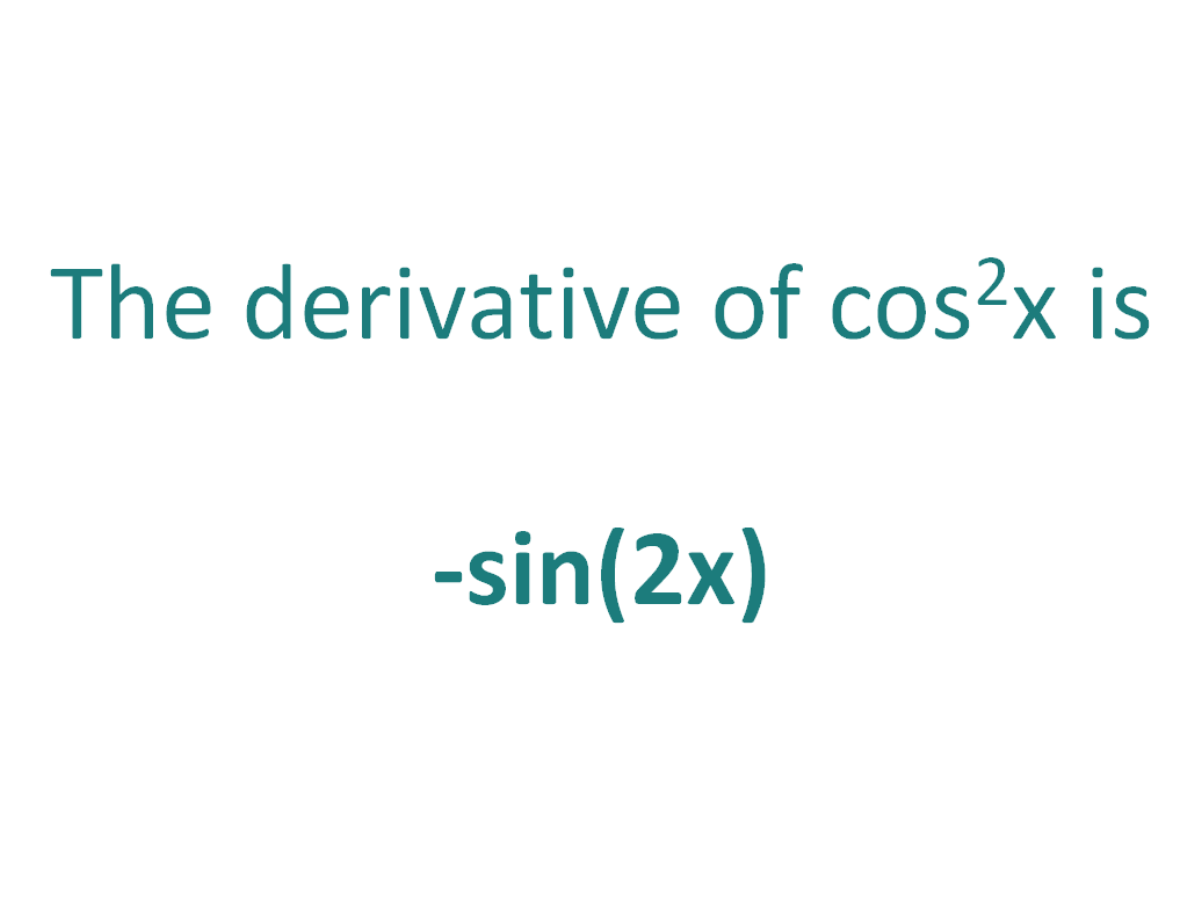



The Derivative Of Cos 2x Derivativeit
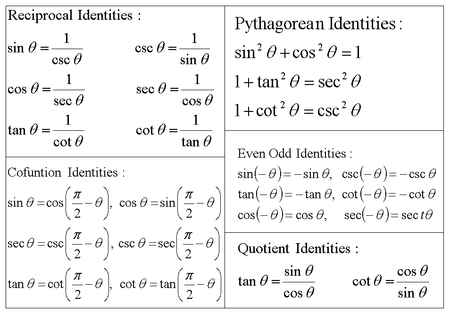
Sine = Opposite / Hypotenuse Cosine = Adjacent / Hypotenuse sin x / cos x = tan x cos x / sin x = cot x = 1 / tan x sec x = 1 / cos x csc x = 1 / sin x sin 2 x cos 2 x = 1 tan 2 x 1 = sec 2 x = 1 / cos 2 x cot 2 x 1 = csc 2 x = 1 / sin 2 x Reduction Formulas sin (90 x) = cos x cos (90 x Law of Cosines a 2 = b 2 c 2 2bc√画像をダウンロード tan^2xsec^2x in terms of sine and cosine Tan^2xsec^2x in terms of sine and cosine sec^2 x tan^2 x = 1 Note that sin^2 x cos^2 x = 1 Hence cos^2 x = 1 sin^2 x and we find sec^2 x tan^2 x = 1/cos^2 x sin^2 x/cos^2 x color(white)(sec^2 x tan^2 x) = (1 sin^2 x)/cos^2 x color(white)(sec^2 x tan^2 x) = cos^2 x/cos^2 x color(white)(sec^2 x tan^2 x) = 1



What Is The Expansion Of Sin 3x And Cos 3x Quora




Integrate Sec 2x Method 2
Sine, cosine, secant, and cosecant have period 2 π while tangent and cotangent have period π Identities for negative angles Sine, tangent, cotangent, and cosecant are odd functions while cosine and secant are even functions Ptolemy's identities, the sum and difference formulas for sine and cosine Double angle formulas for sine and cosineProving $\frac{\cos 2x}{1\sin 2 x} = \sec 2 x \tan 2x$ 0 If $\sec(t) = a 1/(4a)$, prove that $\sec(t) \tan(t) = 2a$ or $1/(2a)$ 1 Expressing $\cos(x)$ and $\sin(x)$ in terms of $\tan(\frac{1}{2} x)$ 3 Simplifying $\frac{\sin x\sin x\tan^2x}{\tan x}$ to $\sec x$ 0 Simplifying $\sec^2 x\tan^2 x$



1




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube




How To Take The Derivative Of Tan X Video Lesson Transcript Study Com




Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com




Powers Of Trigonometric Functions




Trigonometric Identity With Pythagorens Sec 2x Sin 2x Cos 2x Tan 2x Youtube




Solved 2 Prove The Following Trig Identities A Prove Tan Chegg Com




Double Angle Formulas What Are Double Angle Formulas Examples




Trigonometry Reciprocal Identities Expii




How Do You Prove 2tan X Sec X Cos 2x Sin 2x 1 Sin X Cos 2x Sin 2x 1 Sin X Socratic




How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero
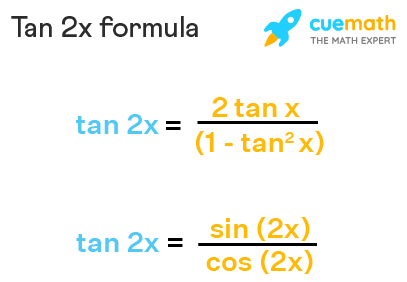



Tan 2x Formula What Is Tan 2x Formula Examples
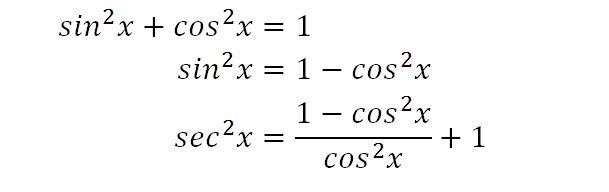



Integrate Sec 2x Method 2
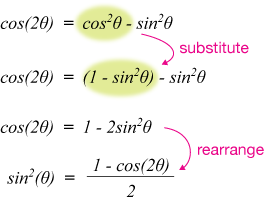



Trig Integrals Trig Substitution




Tangent Half Angle Formula Wikipedia




Derivative Of Tan X Sec X Tan X More



What Is The Integral Of Tanx Sec 2x E Tanx Quora




Solved Write The Expression In Terms Of Sine And Cosine And Chegg Com




Integration Calculus 2
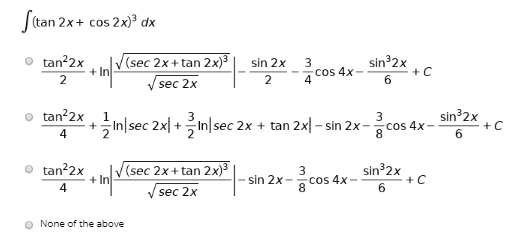



Answered Stan 2x Cos 2x Dx Tan 2x 2 V Sec 2x Bartleby



Proving Identities Trigonometry Socratic
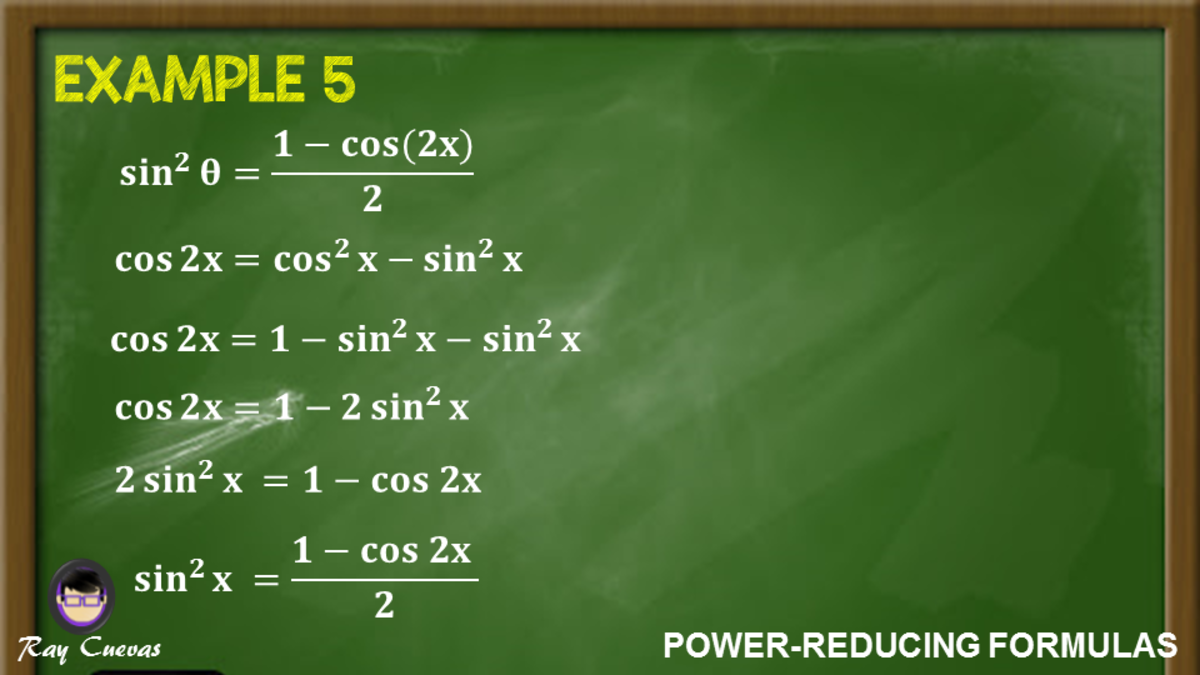



Power Reducing Formulas And How To Use Them With Examples Owlcation




Jpsaepictlqtj Tan 2x Formula Tan 2x Formula In Terms Of Cos X




Weierstrass Substitution Wikipedia



2



1




Tangent Half Angle Formula Wikipedia




Tangent Half Angle Formula Wikipedia



What Is Integral Of Sin2x Tan2x Quora
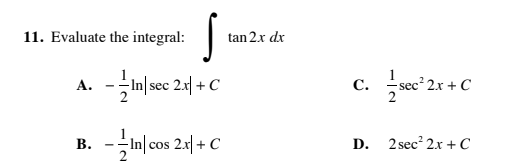



Answered 11 Evaluate The Integral Tan 2x Dx A Bartleby
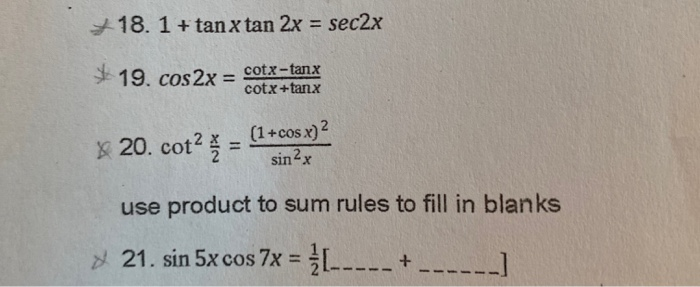



Solved 18 1 Tan X Tan 2x Sec2x 19 Cos2x Cotx Tank Chegg Com
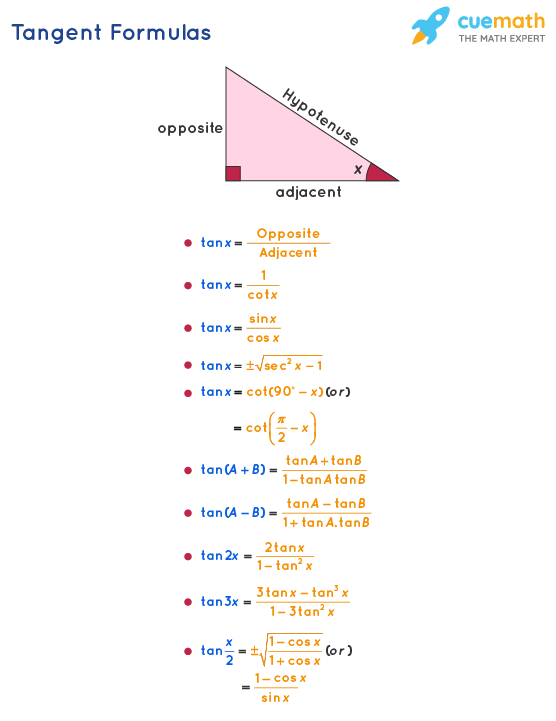



Tangent Formula What Are Tangent Formulas Examples




Copyright C Cengage Learning All Rights Reserved 7 Techniques Of Integration Ppt Download




2 Sin Inverse X Formula In Terms Of Cos Elton Reynold
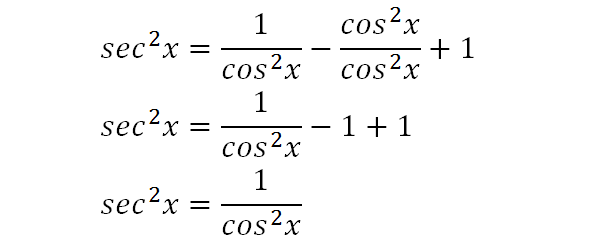



Integrate Sec 2x Method 2




Derive 1 Tan 2x Sec 2x And 1 Cot 2x Text Cosec 2x Geometrically Mathematics Stack Exchange




Trigonometric Functions Introduction Sine Cosine Videos And Examples



1



Tan2x 1 ただの悪魔の画像




Sin 2x Formula What Is Sin 2x Formula Examples




Answered 3 1 Tanx Tan 2x Sec 2x S Bartleby




Misc 8 Tan X 4 3 Find Sin X 2 Cos X 2 And Tan X 2




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube




bestpictjcry Tan 2x Tan 2x



Relating Trigonometric Functions Trigonometry Socratic




Ch 7 Trigonometric Identities And Equations Ppt Video Online Download




Tan 2x Formula What Is Tan 2x Formula Examples




Using Trigonometric Identities Video Khan Academy
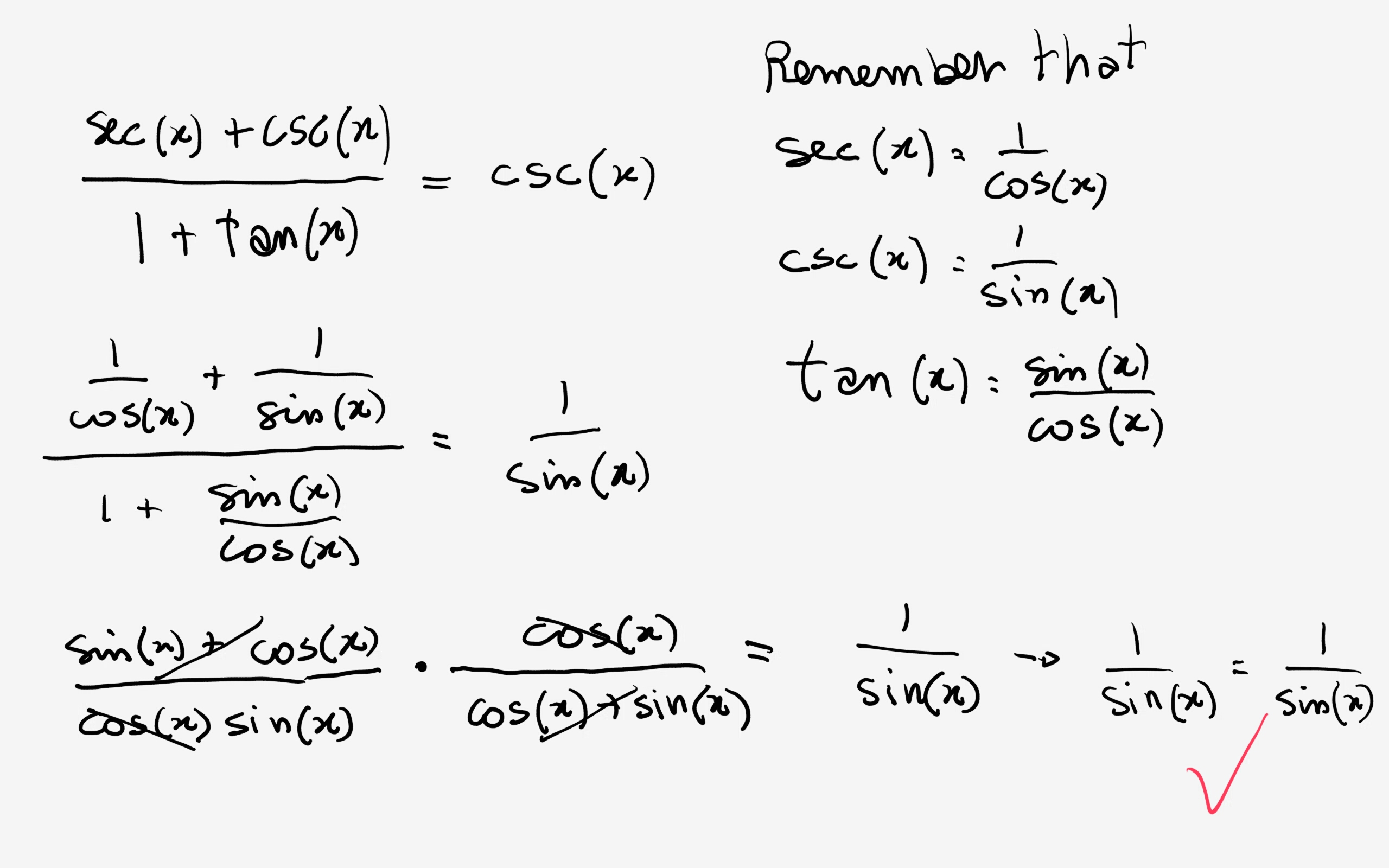



How Do You Prove Sec X Csc X 1 Tan X Csc X Socratic
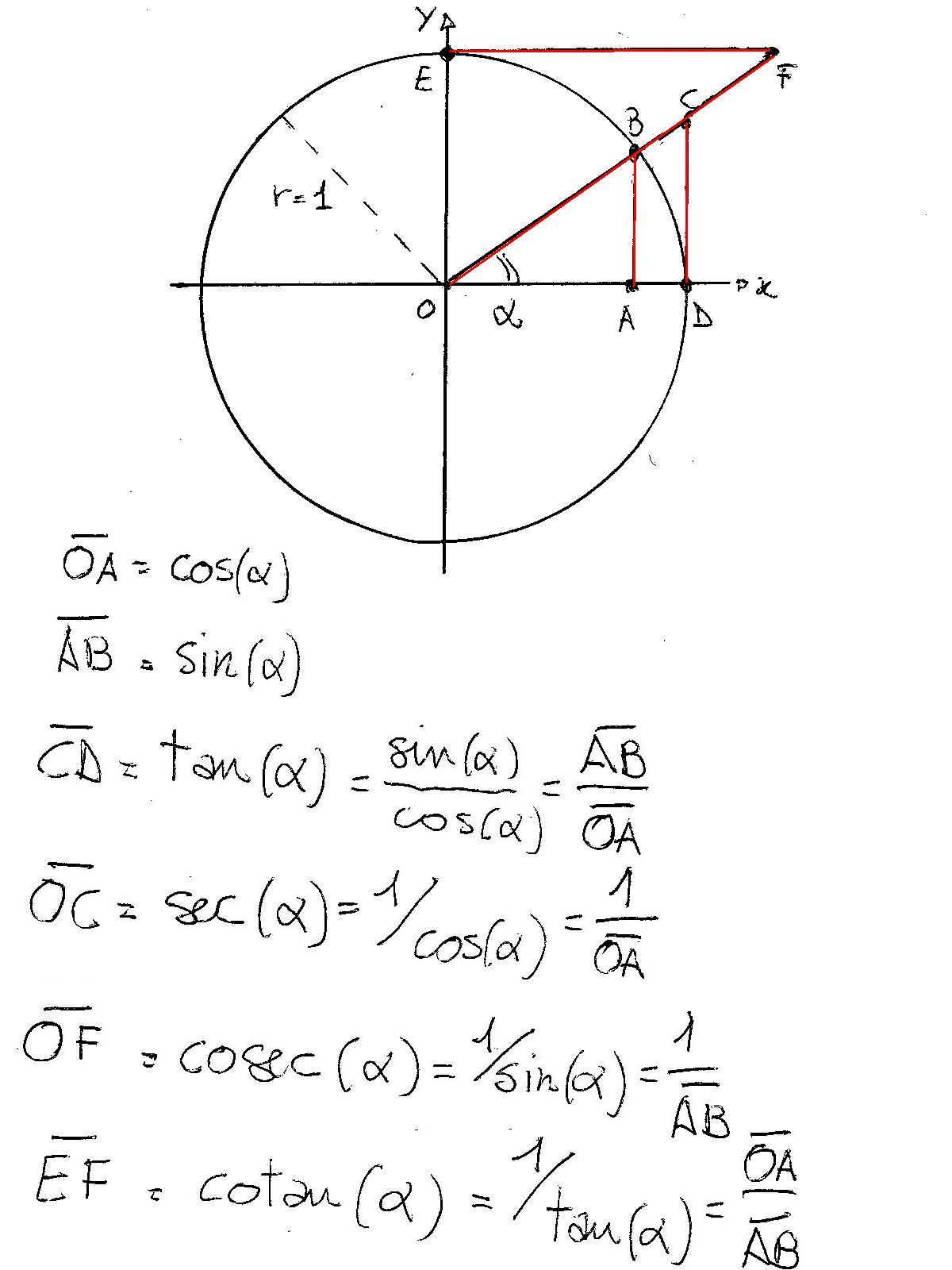



Basic Trigonometric Functions Trigonometry Socratic




Factor The Expression Then Use Fundamental Identities To Simplify Cos 2x Sec 2x Cos 2x Study Com
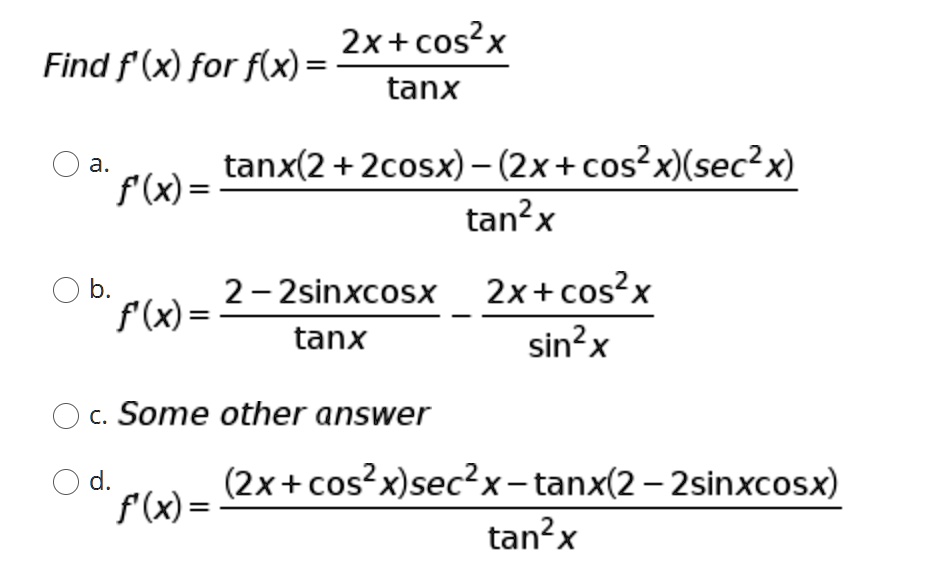



Solved 2xtcos X Find F X For F X Tanx Tanx 2 2cosx 2x Cos X Sec2 X F X Tan X B 2 2sinxcosx F X Tanx 2xtcos X Sin X C Some




How To Find The Inverse Of A Trig Function Dummies




Expressing Sin X And Cos X In Terms Of Tan X Youtube




Sample Problems Cos 2 X Tan2 X Tan 2 Csc 2 Tan Sec X Tan X Cos X Sin 4 X Cos 4 X 1 2 Cos 2 X Pdf Free Download



bestpictjcry Tan 2x Tan 2x




9 1 Identities And Proofs Ppt Download




Tan2x 1 ただの悪魔の画像
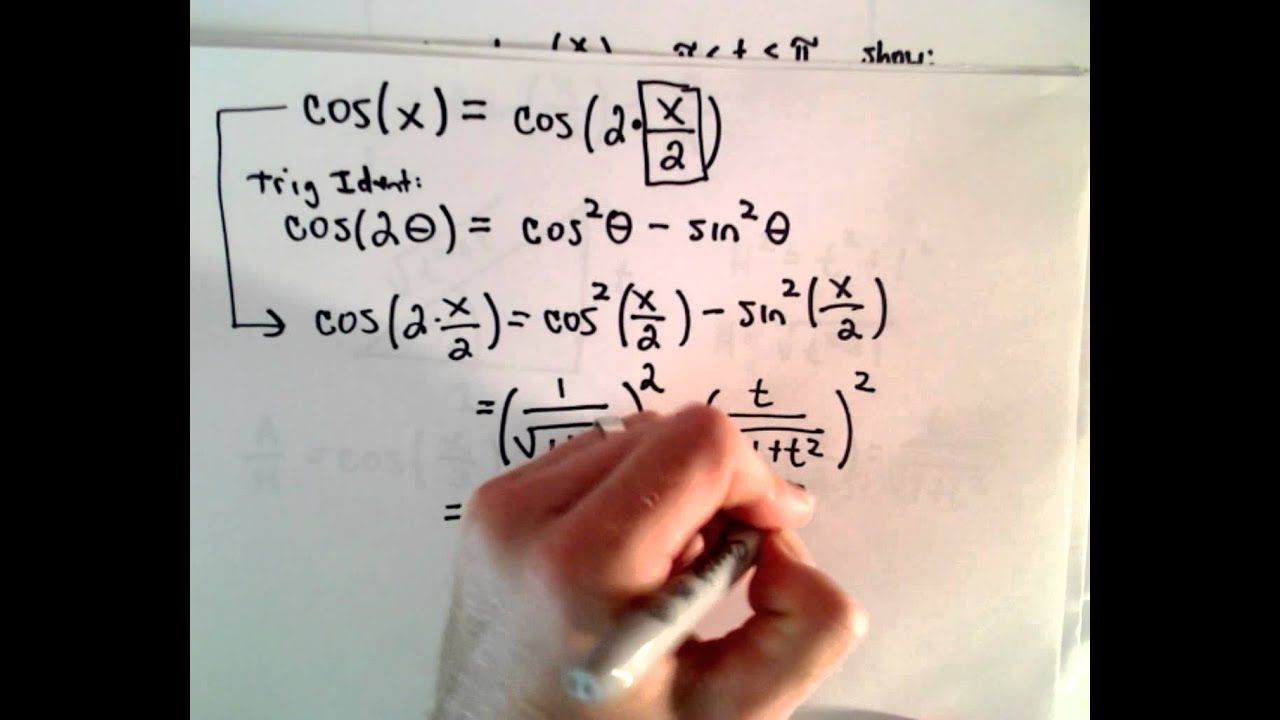



Integrate Rational Function Of Sine And Cosine T Tan X 2 Part 1 Youtube




7 2 Trigonometric Integrals Ppt Download




Tan2x 1 ただの悪魔の画像



What Is The Formula Of Tan2x Quora




Precalc Wup 216 Using Trig Identities 2 Simplify



What Is The Formula Of Tan2x Quora



bestpictjcry Tan 2x Tan 2x




Powers Of Trigonometric Functions



2
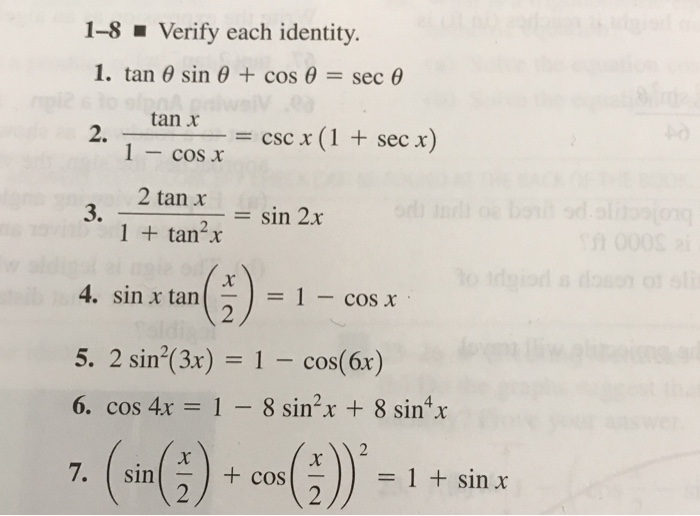



Solved 1 8 Verify Each Identity Sec 8 1 Tan 8 Sin 8 Chegg Com




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic
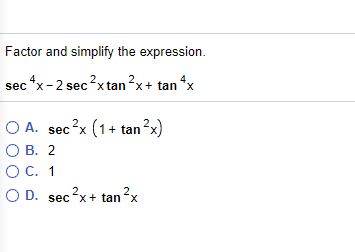



Solved Factor And Simplify The Expression Sec 4 X 2 Chegg Com




Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube




Verify Each Trigonometric Equation By Substituting Identities To Match The Right Hand Side Of The Brainly Com
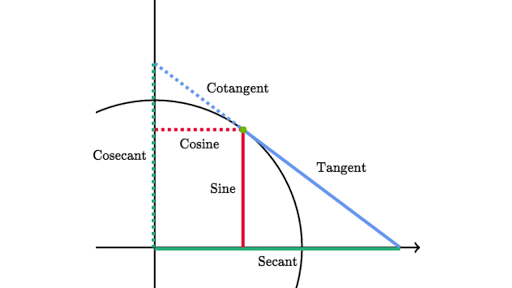



Trig Identity Reference Article Khan Academy




Warm Up 1 Sin 2 X Sec 2 X Cos 2 X Sec 2 X 1 Ppt Download




Sec2x In Terms Of Tanx Trig Identity Youtube




Cos 2x Formula Derivation Examples What Is Cos 2a Formula




Derivative Rules For Trigonometric Functions




Solved Prove The Identity 2 Sin X Cos X Tan 2x 2 Chegg Com
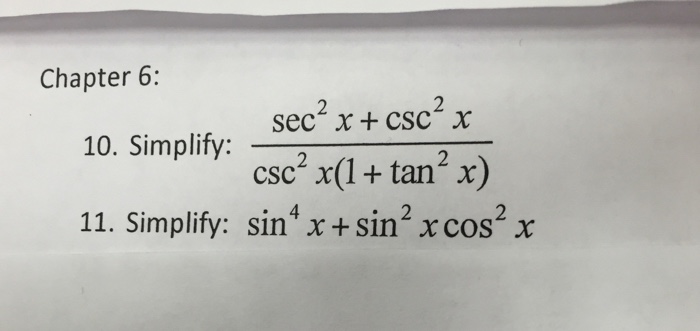



Solved 10 Simplify Sec 2x Csc 2x Csc 2x 1 Tan 2x 11 Chegg Com



No comments:
Post a Comment